Material Builder - Theory Section

The material builder is a tool to create new materials layer by layer. Each layer is created with an empirical model of that particular layer type. The layers are then assembled with a transfer matrix method. The output is the reflection coefficient/surface impedance of the construction as a whole. We can take an example of a material which is assembled like this:

Here the layers are added recursively from the rigid backing to the surface of the material assemble using the transfer matrix method as detailed in [1].

With the following transfer matrix equation:

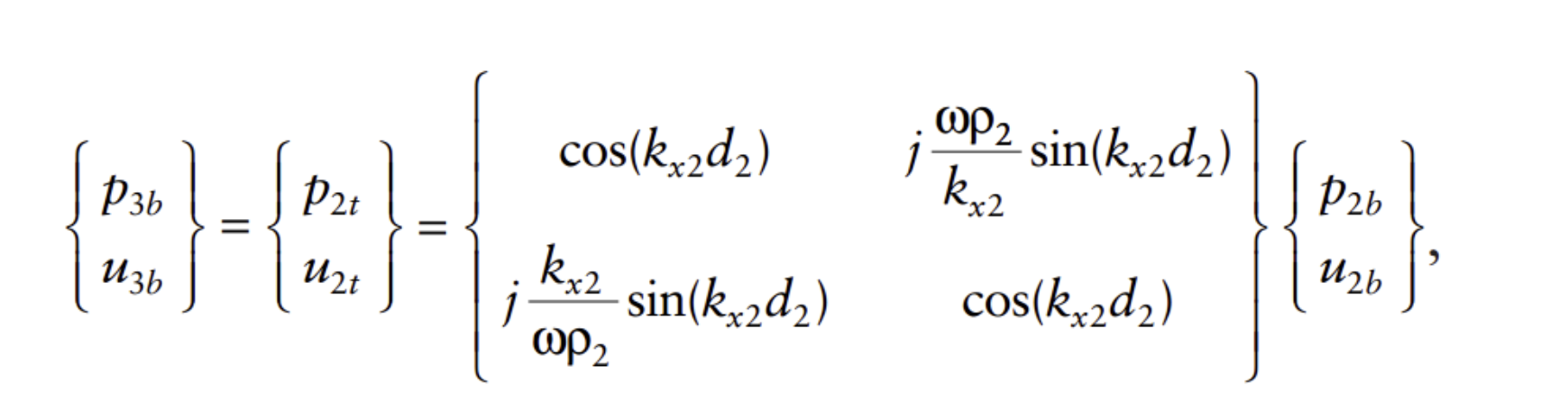
"Where $p_{2b}$ and $u_{2b}$ are the pressure and particle velocity, respectively, at the bottom of the second layer; for velocity, this is defined to be in the x direction; $p_{3b}$ and $u_{3b}$ are the pressure and particle velocity, respectively, at the bottom of the third layer; $p_{2t}$ and $u_{2t}$ are the pressure and particle velocity, respectively, at the top of the second layer; $d_2$ is the thickness of the layer 2; $\rho_2$ is the density of layer 2; and $u_{x2}$ is the x direction component of the complex wavenumber for the 2nd layer and $z_{c2}$ the corresponding characteristic impedance." [1]

The equation above is a recursive equation which enables us to derive the surface impedance, layer by layer. Using this methodology we can relate the surface impedance at the top of layer 2, $z_{s2}$, to the impedance at the top of layer 1, $z_{s1}$ [1].

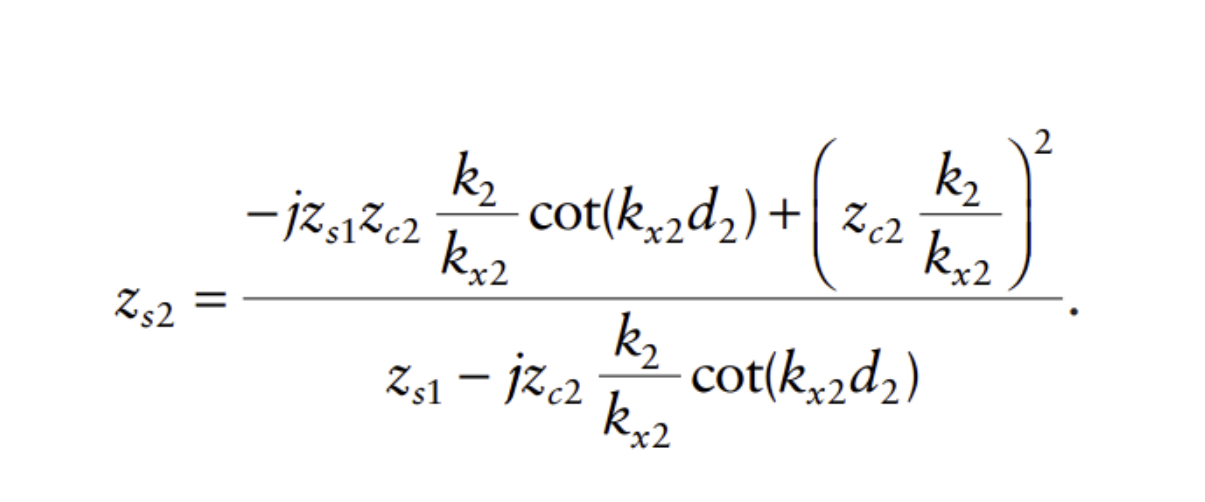
The porous layer is modelled using the so called Miki's model [2]. It is an empirical model in which the characteristic impedance normalized with respect to air is:

$$Z(f) = R(f) + jX(f)$$

With

$$R(f)=1+0.070(f/σ)^{-0.632}$$

$$X(f)=-0.107(f/σ)^{-0.632}$$

And the propagation constant:

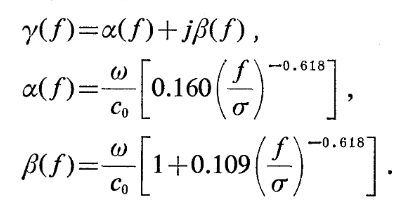
Where $σ$ is the flow resistivity of a material.

Miki's model is most valid for for glasswool and rockwool with flow resistivity in the range of 1000-50.000 $Pas/m^2$. The validity of the model is the strongest in the following frequency range [3]:

$$0.01 ≤ f*\rho_p/σ_p ≤ 1$$

Where $f$ is the frequency, $\rho_p$ is the density of the porous layer in $kg/m^3$ and $σ_p$ is the flow resistivity of the porous layer in $Pas/m^2$.

[1] Cox, T. J., & D’Antonio, P. (2016). Acoustic absorbers and diffusers: Theory, design and application (3rd ed.). CRC Press.

[2]Y. Miki, ''Acoustical properties of porous materials — Generalizations of empirical models —,'' J. Acoust. Soc. Jpn. (E), 11, 25–28 (1990).

[3] COMSOL. About the Poroacoustics Models. COMSOL Documentation. Accessed October 11, 2024. doc.comsol.com/5.5/doc/com.comsol.help.aco/aco_ug_pressure.05.144.html#1452005.