The Image-Source Method
The image-source method (ISM) is a widely used method to model the propagation and reflection of acoustic waves[2]. The basic concept is to mirror the original source across each of the planes in the model, thereby creating an image source. The geometrical model of the space generally consists of many planes, that each will create an image source. After mirroring the original source point across all planes, the visibility of the reflection path to the receiver can be verified by tracing a ray backward. This process begins from the receiver point toward the image source, followed by tracing from the intersection point of the ray and the plane back to the original source.
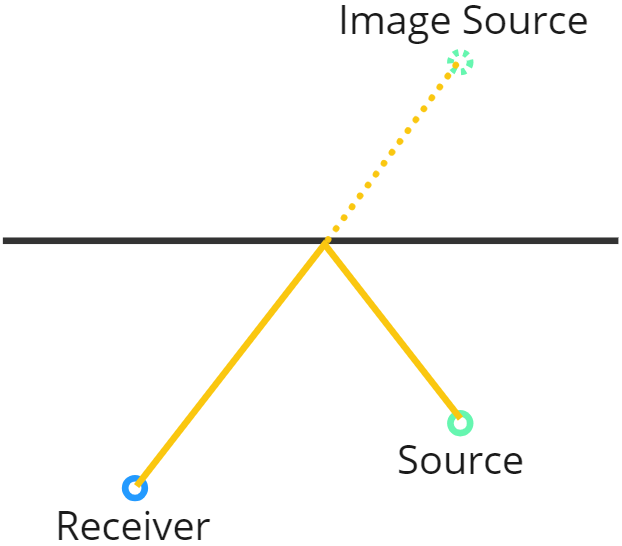
To model the higher order reflections, all of the first order image sources needs to be recursively mirrored across the planes in the same manner as with the original source, forming a tree structure of image sources. After the tree is populated, the valid reflection paths can be checked by backtracing all of the tree branches from the receiver, through the image sources and back to the original source.
Once all the valid reflection paths have been found, Treble's pressure-based solver uses the reflection paths and the impedance and scattering boundary data to model how sound propagates and reflects to reconstruct a response for each reflection. All of these responses are then summed to created the ISM impulse response (ISM-IR).
The effect of the boundary at each reflection accounts for the complex impedance, allowing for the modeling of phase changes introduced by the surface. An additional advantage of using impedance is that it inherently captures the local reaction, naturally incorporating the angle dependence of the reflection. Since the image source method models only the specular component of the response, the scattered energy is subtracted at each reflection.
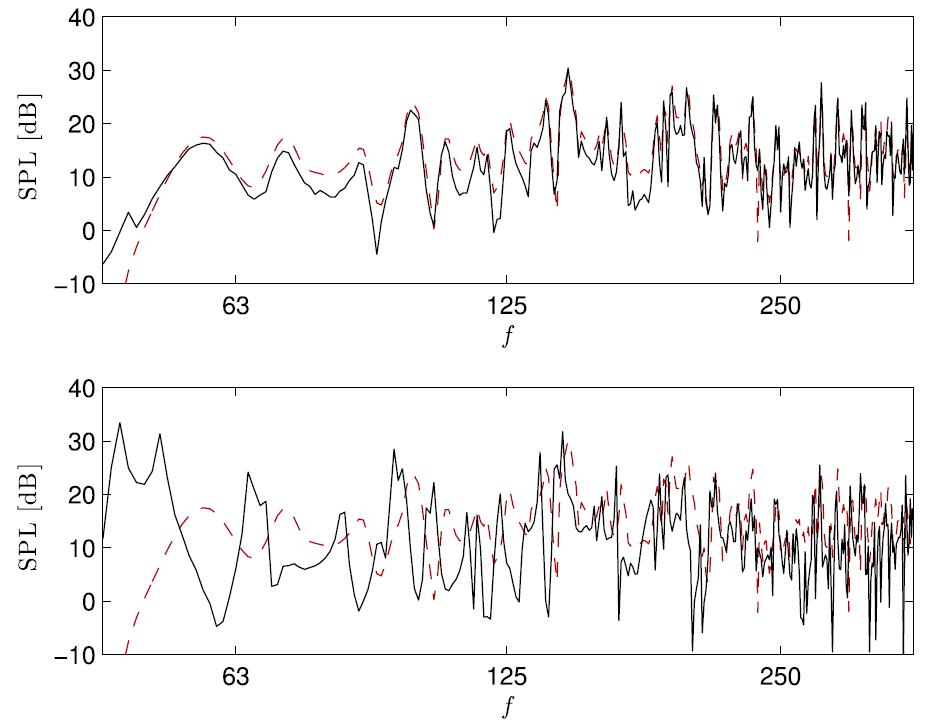
Using the pressure-based methods enabled by having the impedance data for the boundaries is a great advantage and its benefit has been well documented in many scientific publications [2-7]. Below is a comparison of two ISM calculations taken from [2], with a pressure-based reflection coefficient (top figure) and with a random incidence absorption coefficient, i.e., angle-averaged energy quantity showing approximately how much energy is absorbed (bottom figure). The red dashed line is the corresponding wave-based calculation result, which agrees well with the pressure-based ISM with the reflection coefficient data.
References
[1] J. B. Allen and D. A. Berkley. Image method for efficiently simulating small-room acoustics. J. Acoust. Soc. Am., 65:943-950, 1979.
[2] G. Marbjerg, J. Brunskog, C.-H. Jeong, and E. Nilsson. Description and validation of a combined phased acoustical radiosity and image source model for predicting sound fields in rooms. J. Acoust. Soc. Am., 138:1457-1468, 2015.
[3] C.-H. Jeong, J.-G. Ih, and J. H. Rindel. An approximate treatment of reflection coefficient in the phased beam tracing method for the simulation of enclosed sound fields at medium frequencies. Appl. Acoust., 69:601-613, 2008.
[4] J. S. Suh and P. A. Nelson. Measurement of transient response of rooms and comparison with geometrical acoustic models. J. Acoust. Soc. Am., 105:2304-2317, 1999.
[5] A. Wareing and M. Hodgson. Beam-tracing model for predicting sound fields in rooms with multilayer bounding surfaces. J. Acoust. Soc. Am., 118:2321-2331, 2005.
[6] M. Aretz, P. Dietrich, and M. Vorländer. Application of the mirror source method for low frequency sound prediction in rectangular rooms. Acta Acust. united Acustica, 100:306-319, 2014.
[7] Y. W. Lam. Issues for computer modelling of room acoustics in non-concert hall settings. Acoust. Sci. Tech., 26:145-155, 2005.