Scattering
In acoustic simulations, scattering is used to describe how sound interacts with surfaces in a non-specular manner. Real-world surfaces are rarely perfectly smooth, causing reflections to scatter in multiple directions rather than following a purely specular path.
Scattering is quantified using scattering coefficients, which represent the proportion of sound energy that is reflected in directions other than the specular one. It ranges between 0 and 1, where 0 indicates a purely specular reflection, and 1 signifies a fully diffuse reflection. To a large extent, the scattering coefficient is an essential concept in geometrical acoustics (GA) to compensate for the absence of diffraction and other wave-based effects in its fundamental approximations and assumptions.
A surface can be assigned either a single scattering coefficient or a scattering coefficient per octave band. These two input types lead to different behaviors in the solver and are not expected to produce identical results.
Regardless of the input type, the concept of a Trace Scattering Coefficient must be introduced. This coefficient is used exclusively in the ray-radiosity solver, where it determines the new direction of radiosity rays during tracing. It is frequency dependent for per band scattering inputs and frequency independent for single value inputs.
For a per band input, the scattering value is used as is to generate scattering coefficients for each octave band.
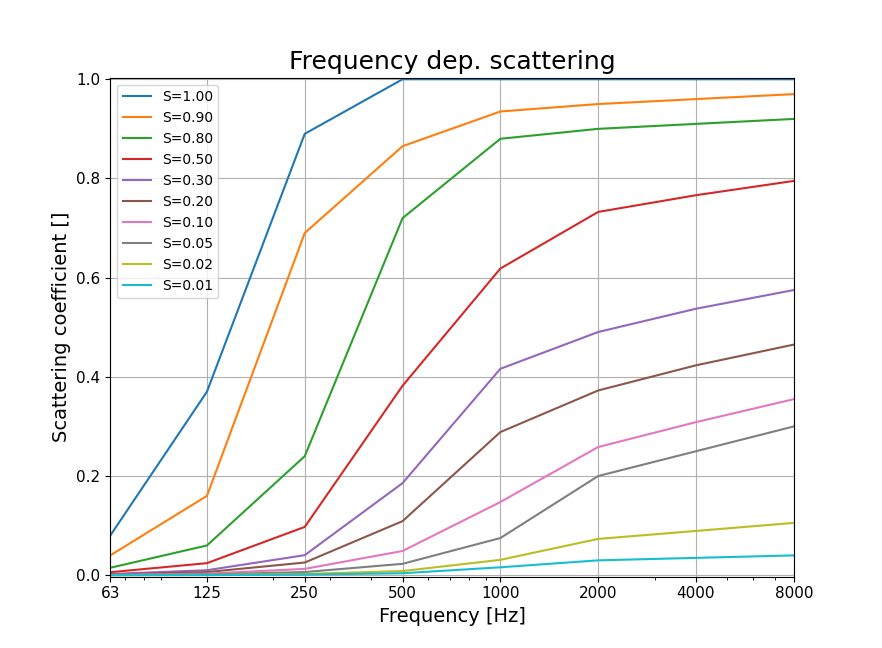
For a single-value input, a different scattering value is extrapolated to generate another type of scattering coefficient for each octave band, as illustrated in the figure below [1]. This value determines the orientation of the Lambert distribution balloon, as explained below.
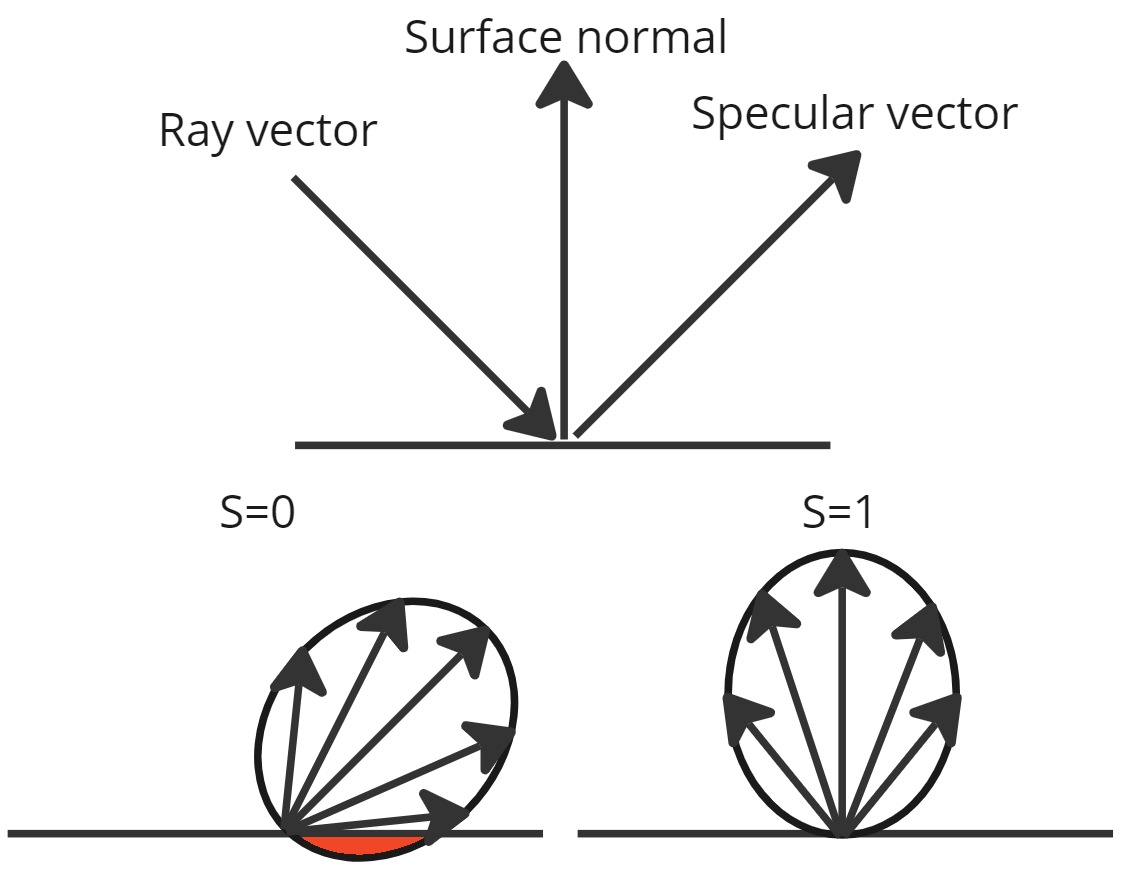
The Ray-Radiosity solver uses the latter scattering coefficient during the step where energy is traced from the surface intersection points to the receivers. The coefficient scales the amount of energy being registered, with the Lambert distribution angled towards either the surface normal (for scattering=1) or the specular vector (for scattering=0). To conserve energy, the distribution is scaled by the factor corresponding to the portion of the distribution that falls behind the surface. While the figure illustrates the 2-Dimensional case, the same principles apply similarly in the 3D case.
Finally, the Image Source method will apply either the extrapolated curve or the input octave band values when subtracting the scattered energy.
References
[1] Odeon. ODEON Room Acoustics Software user’s manual version 18. Accessed October 11, 2024.