Import Material

New materials can be imported in the Material Library using the Material Fitting Engine. This process supports user-provided values of full-octave or third-octave band random-incidence absorption coefficients; third-octave surface impedance values, or third-octave reflection coefficients. For more information on the differences between the three types of user-inputs, please reference the technical reference pages on Material Inputs in Treble. The three ways of importing materials and how they make their way through the Treble Material Engine is visualized below.

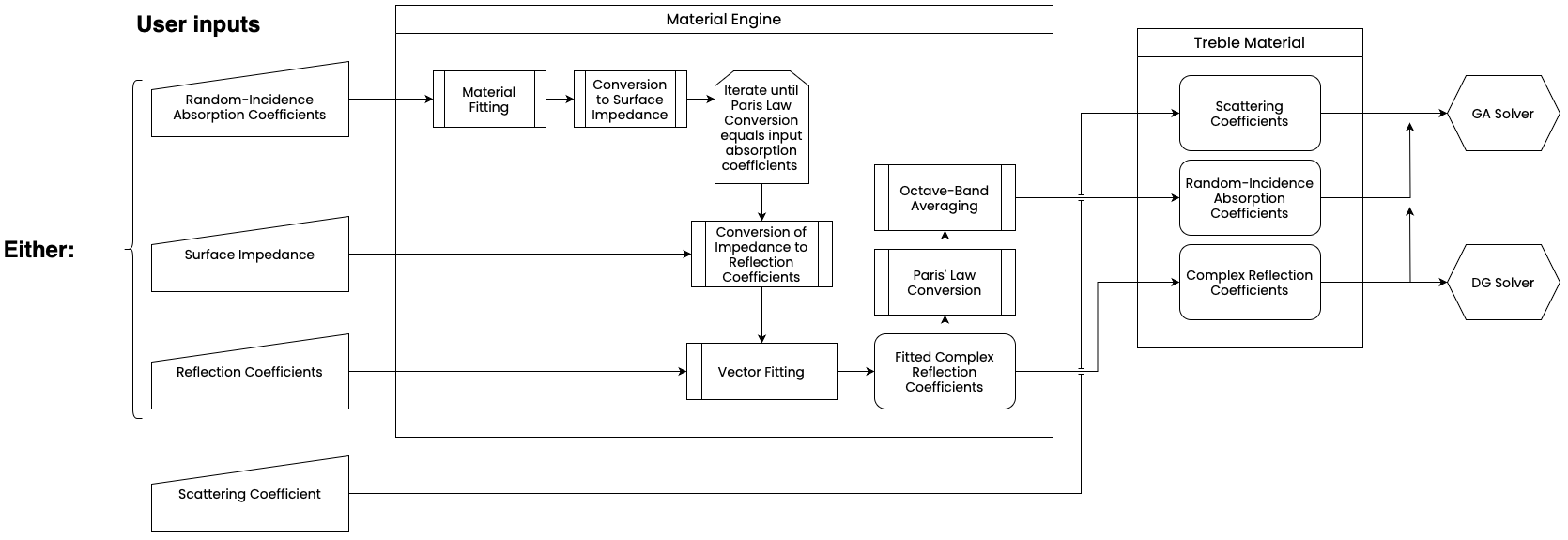
Importing a new material into the Treble Material Library follows three steps.

1. Define a MaterialDefinition object
2. Perform material fitting on the MaterialDefinition and validate the fit
3. Add the fitted material to the library

The following sections will examine each step in more detail.

Material Definition

The core of the material import process is the creation of a MaterialDefinition object, which allows you to provide a unique name and description to the imported material, assign it to a category, specify the default scattering coefficient, and select the input type.

A MaterialDefinition object contains the following properties:

Property	Type	Description	Example value
name	string	The human-friendly material name.	'Acoustic plaster 68 mm thick'
description	string	Additional information associated with the material.	'Acoustic plaster with thickness of 50-70 mm'
category	string	The category to which the material will be assigned.	'Gypsum'
defaultScattering	float	A single value numeric float between 0 and 1 used within the geometrical acoustics solver.	0.15
materialType	enum	Type of input expected by the fitting engine.	treble.MaterialRequestType.full_octave_absorption, treble.MaterialRequestType.third_octave_absorption, treble.MaterialRequestType.surface_impedance, treble.MaterialRequestType.reflection_coefficient
coefficients	array	The array of 8 or 24 elements (full-octave or third-octave) used in the material fitting	[0.2, 0.45, 0.3, 0.65, 0.8, 0.82, 0.84, 0.88]
specificImpedance	bool	Only available when the materialType is treble.MaterialRequestType.surface_impedance	True, False

All values must be provided when creating a MaterialDefinition, except for the specificImpedance, which is only required when the materialType is treble.MaterialRequestType.surface_impedance.

The following code snippet creations a MaterialDefinition using full octave-band absorption coefficients.

# Example input coefficients, full octave band absorption coefficients
absorption_coefficients = [0.2, 0.45, 0.3, 0.65, 0.8, 0.82, 0.84, 0.88]

# Create the material definition object
material_definition = treble.MaterialDefinition(
    name="Example material from absorption coefficient",
    description="Example material",
    category=treble.MaterialCategory.other,
    default_scattering=0.23,
    material_type=treble.MaterialRequestType.full_octave_absorption,
    coefficients=absorption_coefficients,
)

Meanwhile, this code snippet uses complex surface impedance, and specifies that the coefficients provided are specific impedances:

import numpy as np
# Example one third octave-band impedance values
impedance_values = [(342.4274-3147.8j), (358.6007-2515.4j),
    (344.2741-1956.7j), (341.8532-1553.4j), (358.8722-1239.6j),
    (347.5786-947.6j), (351.247-739.8j), (359.7332-567.9j),
    (360.8415-424.4j), (373.8132-300.6j), (401.4228-195.3j),
    (441.0573-117j), (509.9243-62.2j), (574.991-83.3j),
    (580.3443-146.5j), (506.0581-180.6j), (426.3545-140.3j),
    (444.5958-62.7j), (465.5363-75.3j), (449.401-75.3j),
    (436.9184-64.2j),(428.9319-53.4j), (424.0636-42.5j),
    (420.8714-33.7j)
    ]

impedance_values = np.asarray(impedance_values)
# Create the material definition object
material_definition = treble.MaterialDefinition(
    name="Third octave surface impedance",
    description="Imported material",
    category=treble.MaterialCategory.curtains,
    default_scattering=0.4,
    material_type=treble.MaterialRequestType.surface_impedance,
    coefficients=impedance_values,
    specific_impedance=True
)

Material Fitting

The MaterialDefinition object may now be sent to the material engine. As can be seen from the following schematic, the definition's materialType property determines the calculations performed on the input coefficients in order to create a fitted material.

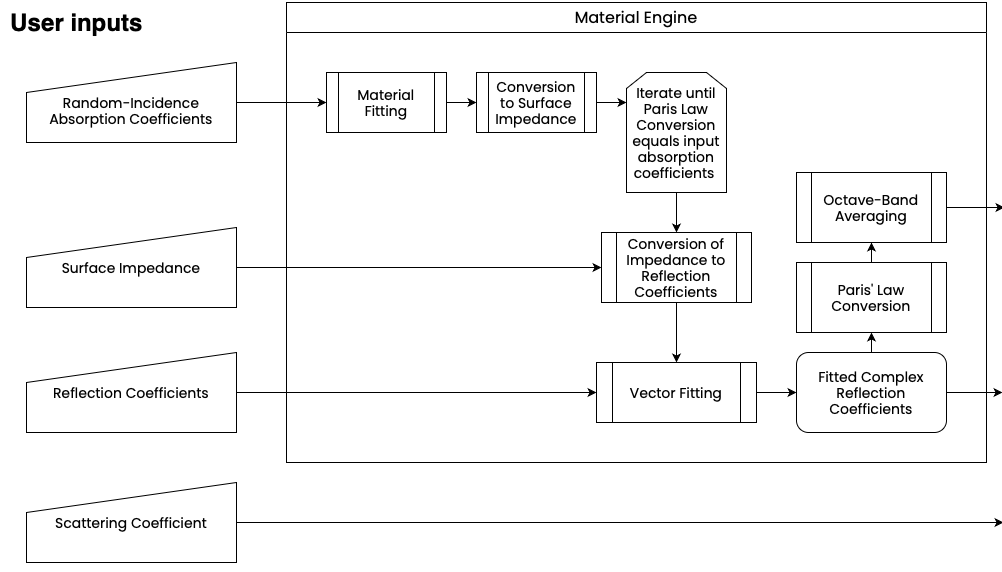
Absorption coefficient inputs

When a user provides absorption coefficients to the material engine, an iterative fitting is performed on the input data, where an initial fit is converted to a surface impedance value. This intermediate impedance value is then converted back to a random-incidence absorption coefficient via Paris' Law, and the resulting coefficients are compared with the initial input. This iterative process continutes until the derived absorption coefficients are equivalent to the input data: at this point, the appropriate one-third octave-band impedance values are passed to the next stage of the calculation.

Impedance values

User-provided impedance values bypass the impedance derivation step that applies to absorption coefficients. Whether input directly as a part of the material definition or derived from the provided absorption coefficients, the material engine converts the impedance into complex reflection coefficients, which are then passed to the next step of the process.

Reflection coefficients

Reflection coefficients, either user-defined or derived from other inputs are sent into a vector-fitting process, described in greater detail in the technical reference page Material Inputs in Treble. After enforcing passivity, the resulting fitted complex reflection coefficients are assigned to the fitted material. Finally, the fitted reflection coefficients are converted into octave-band random-incidence absorption coefficients via Paris' Law.

Material fitting outputs

The material fitting process outputs a MaterialDto containing the properties presented in the Introduction to Materials page. The material object's properties may be queried like a material within the Material Library, but at this stage, the material has not yet been saved to the library.

tip

Material fitting within Treble is non-deterministic, and variations may be observed in fit-refit comparisons. We recommend that you include a visual or mathematical inspection step after fitting a material and before creating the material to ensure the best results.

Example: Fitting with Absorption Coefficients

The following is a worked example of a material fitting using full octave-band absorption coefficients.

import numpy as np
import matplotlib.pyplot as plt
# full-octave band definitions
f_axis_oct = np.asarray([63, 125, 250, 500, 1000, 2000, 4000, 8000])

# Example input coefficients
absorption_coefficients = [0.2, 0.45, 0.3, 0.65, 0.8, 0.82, 0.84, 0.88]

# Create the material definition object
material_definition = treble.MaterialDefinition(
    name="Full octave absorption material",
    description="Imported material",
    category=treble.MaterialCategory.curtains,
    default_scattering=0.4,
    material_type=treble.MaterialRequestType.full_octave_absorption,
    coefficients=absorption_coefficients,
)

# Material fitting, nothing is saved in this step
fitted_material = tsdk.material_library.perform_material_fitting(material_definition)

# Retrieve the absorption coefficients from the fitted material
fitted_material_abs = fitted_material.absorptionCoefficients

# Visualise the fitting results
plt.semilogx(f_axis_oct, absorption_coefficients,label='Original Coefficients')
plt.semilogx(f_axis_oct, fitted_material_abs, label='Fitted Coefficients')
plt.grid(which='both')
plt.xlim([50, 10000])
plt.ylim([0,1])
plt.xlabel('Frequency, Hz')
plt.ylabel('Absorption Coefficient')
plt.title('Input vs. Fitted Absorption Coefficients')
plt.legend()

Example: Fitting with Reflection Coefficients

The following is a worked example of a material fitting using complex reflection coefficients.

import json
import numpy as np
import matplotlib.pyplot as plt
# Frequency array for plotting
f_axis_thirdoct = np.asarray([63, 80,
                            100, 125, 160,
                            200, 250, 315,
                            400, 500, 630,
                            800, 1000, 1250,
                            1600, 2000, 2500,
                            3150, 4000, 5000,
                            6300, 8000, 10000,
                            12500])

# example input reflection coefficients
reflection_coefficients = [(0.9405-0.248j),(0.908-0.3j),
(0.858-0.367j),(0.7911-0.43j),(0.7012-0.48j),
(0.5747-0.53j),(0.4423-0.54j),(0.3062-0.51j),
(0.1797-0.45j),(0.0842-0.35j),(0.0412-0.23j),
(0.0509-0.13j),(0.1093-0.06j),(0.1701-0.07j),
(0.1864-0.12j),(0.1349-0.17j),(0.0429-0.16j),
(0.0422-0.07j),(0.0669-0.08j),(0.0497-0.083j),
(0.0339-0.073j),(0.0231-0.062j),(0.016-0.05j),
(0.0113-0.04j),
]

# Create the material definition object
material_definition = treble.MaterialDefinition(
    name="Material from reflection coefficient",
    description="Imported material",
    category=treble.MaterialCategory.curtains,
    default_scattering=0.4,
    material_type=treble.MaterialRequestType.reflection_coefficient,
    coefficients=reflection_coefficients
)

# Material fitting, nothing is saved in this step
fitted_material = tsdk.material_library.perform_material_fitting(material_definition)

# Retrieve the fitted reflection coefficients
fitted_material_refl_json = json.loads(fitted_material.materialMetadataJson)
fitted_material_refl = np.asarray(fitted_material_refl_json['RealReflectionCoefficient']) + \
                        1j * np.asarray(fitted_material_refl_json['ImagReflectionCoefficient'])

# Visualise the fitting results
plt.semilogx(f_axis_thirdoct, np.real(reflection_coefficients),label='Original Coefficients, Real')
plt.semilogx(f_axis_thirdoct, np.imag(reflection_coefficients),label='Original Coefficients, Imaginary')
plt.semilogx(f_axis_thirdoct,np.real(fitted_material_refl), label='Fitted Coefficients, Real')
plt.semilogx(f_axis_thirdoct,np.imag(fitted_material_refl), label='Fitted Coefficients, Imaginary')
plt.grid(which='both')
plt.xlim([50, 16000])
plt.xlabel('Frequency, Hz')
plt.ylabel('Reflection Coefficient')
plt.title('Input vs. Fitted Reflection Coefficients')
plt.legend()

Create Material

When you are ready to finalise the fitted material and add it the material library, call the material library function create on the fitted material:

this_created_material = tsdk.material_library.create(fitted_material)
dd.as_tree(this_created_material)

Once you have created a material, the material has been added to your organisation's local Material Library and may be used identically to the default materials availabe in the Material Library upon installation.

To retrieve the newly created material's properties, you can use the same methods presented in the Material Introduction to interact with them.

# access this_created_material's Material Name
this_created_material.name

# access this_created_material's Material ID
this_created_material.id

# check the this_created_material's category
this_created_material.category

In the following snippet, we check that the imported material has been included in the material library.

# get this_created_material's unique ID
mat_id = this_created_material.id

# fetch the material by its ID
new_mat = tsdk.material_library.get_by_id(mat_id)
assert new_mat